
 |
|
|
Abstracts presentations phd studentsFaizan Ahmed University of Twente F.Ahmed@utwente.nl Supervisor Abstract Copositive programs (CP) are of the form: 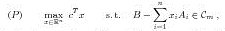
where C_m denotes the cone of copositive matrices: C_m := {A \in S_m|z^T Az \ge 0 for all z \in R^m_+}. Here, S_m denotes the set of symmetric m x m-matrices. During the last years copositive programming has attracted much attention due to the fact that many difficult (NP-hard) quadratic and integer programs can be reformulated equivalently as CP (see e.g., [4]). Linear semi-infinite programs (LSIP) are of the form: 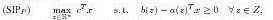
with an (infinite) compact index set Z \subset R^m and continuous functions a : Z --> R^n and b : Z --> R. In this presentation we will briefly discuss copositive and semidefinite programming relaxations of combinatorial optimization problems. Then we will turn our attention to the connections between CP and LSIP. We will view copositive programming as a special instance of linear semi-infinite programming. Discretization methods are well known for solving LSIP (approximately). The connection between CP and LSIP will lead us to interpret many approximation schemes for CP as a special instance of discretization methods for LSIP. The error bound for these approximation schemes in terms of the mesh size will be analysed in detail.
References
Agata Banaszewska Wageningen University agata.banaszewska@wur.nl Supervisor Abstract Every day dairy manufacturers face numerous challenges resulting both from complex and unsteady dairy markets, and from specific characteristics of dairy supply chains. To maintain a competitive position on the market companies must look beyond standard solutions that are currently used in practice. This paper presents a Dairy Valorization Model (DVM), which can serve as a decision support tool for mid-term allocation and production planning. The developed model is used to indicate the optimal product portfolio composition. In other words, the model allocates raw milk to the most profitable dairy products, while taking important constraints into account, i.e.: recipes, composition variations, dairy production interdependencies, seasonality, demand, supply, capacities, transportation. Two important elements that influence the valorization of raw milk are the seasonality of raw milk's composition and supply, and the re-use of by-products. The production of dairy products is based on the composition, i.e. the level of dry matter, fat and protein. Therefore, the variable composition of raw milk affects the choice of products to be produced. Furthermore, by-products obtained while producing certain dairy products can be further used as an input for the production of other dairy products. The optimal re-use of these by-products improves the overall raw milk valorization. Current literature does not provide models that take all the enumerated constraints into account. Furthermore, the impact of raw milk's seasonality has not been evaluated yet. The Dairy Valorization Model developed in this paper is additionally used to evaluate this impact. The applicability of the model is verified at the international dairy manufacturer Royal Friesland Campina (RFC).
Remco Bierbooms Eindhoven University of Technology R.Bierbooms@tue.nl Supervisor Abstract In this presentation we consider single- and multi-server production lines consisting of a number of machines or machines in series and a finite buffer between each of the machines. The flow of products behaves like a fluid. Each machine suffers from breakdowns, which are for example caused by failures, changeovers, cleaning etcetera. We are typically interested in the throughput of such production lines. We construct an analytical model, which is an iterative method. The production line is decomposed into subsystems, each subsystem consisting of an arrival workstation, a departure workstation and a buffer in between. We model the up- and down behavior of the arrival and departure machines as continuous-time Markov chains, including possible starvation of the arrival machine and possible blocking of the departure machine. We propose two variants of this model: an algorithm for single-server production lines with generally distributed up- and downtimes, and an algorithm for multi-server production lines with exponentially distributed up- and downtimes. The model is supported by two case studies. The first case is a production line at Heineken Den Bosch, where retour bottles are being filled and processed by 11 machines in series having different machine speeds. The second case is a production line at NXP semiconductors in China, consisting of eight machines in series. A tape with computer chips flows through the machines; at each machine small electronic components are attached to the chips.
Joost Bosman CWI joost.bosman@gmail.com Supervisor Abstract We consider a tandem of two fluid queues. The first fluid queue is a Markov Modulated fluid queue and the second queue has a fixed output rate. We show that the distribution of the fluid, combined in both buffers, corresponds to the distribution of the maximum level of the first buffer. Moreover we show that the distribution of the total fluid converges to a Gumbel (extreme value) distribution. From this result we derive the asymptotic probability that the second buffer becomes empty, for a given time span and initial amount of fluid. This model is motivated by a video streaming application over an unreliable communication network. The results can be used to dynamically control video quality under uncertain and time-varying network conditions.
Harm Bossers University of Twente H.C.M.Bossers@utwente.nl Supervisor Abstract In parametric IC testing, outlier detection is applied to filter out potential unreliable devices. Most outlier detection methods are used in an offline setting and hence are not applicable to Final Test, where immediate pass/fail decisions are required. Therefore, we developed a new bivariate online outlier detection method that is applicable to Final Test without making assumptions about a specific form of relations between two test parameters. An acceptance region is constructed using kernel density estimation. We use a grid discretization in order to enable a fast outlier decision. After each accepted device the grid is updated, hence the method is able to adapt to shifting measurements.
Harmen Bouma University of Groningen H.W.Bouma@rug.nl Supervisor Abstract In this talk we combine Pooling Problems and Inventory Routing Problems into 'Inventory Pooling and Routing Problems'. Both Pooling Problems and Inventory Routing Problems have extensively been studied in literature. In both problems, there are multiple retailers that are periodically supplied by a warehouse. In Inventory Routing Problems it is investigated how much stock should be stored at each retailer such that the sum of inventory costs and transportation costs are minimised. Pooling models on the other hand determine the level of safety stocks and related inventory costs when inventories of retailers are pooled. This implies that between periodic replenishments there is a fixed point in time at which stock may be redistributed among retailers. It is well-known that pooling has a positive effect on costs. However, to the best of our knowledge, existing pooling models do not take transportation costs for redistribution into account. For this reason, we consider the pooling problem with transportation costs, i.e. the Inventory Pooling and Routing Problem. As this is a new type of problem, we start with a very simple model with two identical retailers and one warehouse with a pre-determined distribution route. We assume that demand is normally distributed. This model serves as a basis for more realistic settings in which more retailers are included, in which the route is not fixed or demands differ among retailers.
Serra Caner University of Groningen s.caner@rug.nl Supervisor Abstract Firms are forced to manufacture environmental products due to increasing consumer awareness, environmental activism and legislative pressure. Remanufacturing, a process whose goal is to recover the residual value of used products by reusing the components that are still functioning well, reduces both raw material and energy consumption. In this study we consider cooperation between original equipment manufacturers to increase the efficiency of the reverse channel performance. We mainly focus on two special cases where grand coalition is possible and we determine efficient allocation of gains. We find that the games we consider in both cases are convex and proportional rule is an efficient way to allocate payoffs.
Yanting Chen University of Twente Y.Chen@utwente.nl Supervisor Abstract We consider the invariant measure of a continuous-time Markov process in the quarter-plane. The basic solutions of the global balance equation are the geometric distributions. We first show that a finite linear combination of basic geometric distribution cannot be invariant measure unless it consists of a single basic geometric distribution. Second, we show that a countable linear combination of geometric terms can be an invariant measure only if it consists of pairwise coupled terms. As a consequence, we have obtained a complete characterization of all countable linear combinations of geometric product forms that may yield an invariant measure for a homogeneous continuous-time Markov process in the quarter-plane.
Bart de Keijzer CWI B.de.Keijzer@cwi.nl Supervisor Abstract We study the inefficiency of equilibria for several classes of games when players are (partially) altruistic. We model altruistic behavior by assuming that player i's perceived cost is a convex combination of 1-a_i times his direct cost and a_i times the social cost. Tuning the parameters a_i allows smooth interpolation between purely selfish and purely altruistic behavior. Within this framework, we study altruistic extensions of congestion games, cost-sharing games and utility games. We derive (mostly) tight bounds on the price of anarchy of these games for several solution concepts. Thereto, we suitably adapt the smoothness notion introduced by Roughgarden and show that it captures the essential properties to determine the robust price of anarchy of these games. Our bounds reveal a surprising trend: for congestion games and cost-sharing games, the robust price of anarchy increases with increasing altruism; for valid utility games, it remains constant and is not affected by altruism.
Jan-Pieter Dorsman Eindhoven University of Technology j.l.dorsman@tue.nl Supervisor Abstract In the classical machine-repair model, a machine subject to breakdown typically faces competition for repair facilities with other machines, which leads to dependencies in their downtimes. In this presentation, contrary to the classical machine-repair model, we explicitly consider the queues of products serviced by the machines. This results in a layered queueing network, where the machines have the dual role of being both customers to the repairman and servers for the products. Due to the interaction between the layers, the queues of products are correlated, making exact analysis generally hard. We present an approximation for the marginal queue length distribution of the products by drawing an analogy between the queue of products and a single-server queue with one-dependent server vacations. Using PGFs, we derive the closed-form expression for (an approximation of) the marginal queue length distribution. For the joint queue length distribution, we use the power-series algorithm in order to numerically evaluate the queues of products, which results in highly accurate results, in particular in light traffic.
Hans Ensinck Maastricht University j.ensinck@maastrichtuniversity.nl Supervisor Abstract Tree-width is an important parameter for undirected simple graphs, that indicates how much a graph resembles a tree (For instance, the tree-width of a tree is 1, and the tree-width for a clique of size n is n-1). Once the tree-width for a graph is known, many hard problems become solvable in polynomial or even linear time (they are only exponential in the tree-width). Determining the tree-width of a graph is equivalent to finding a triangulation of that graph, where the size of the largest clique is minimized. Many algorithms for tree-width use an elimination ordering (of vertices) to generate these triangulations. Most of these construct these elimination orderings from beginning to the end. Our algorithm however constructs the elimination orderings the other way around. Using this different approach, we can substantially reduce the number of branches which leads to an algorithm that is comparable in speed to the fastest known algorithm for tree-width.
Lanah Evers TNO lanah.evers@tno.nl Supervisor Abstract Unmanned Aerial Vehicles (UAVs) can provide significant contributions to information gathering in military missions. UAVs can be used to capture both full motion video and still imagery of specific target locations within the area of interest. In order to improve the effectiveness of a reconnaissance mission, it is important to visit the largest number of interesting target locations possible, taking into consideration operational constraints related to fuel usage, weather conditions and endurance of the UAV. Since UAVs operate in a dynamic and uncertain environment, effective UAV mission plans should be able to deal with environment changes and with changing expectations. For instance, the fuel usage between the targets is uncertain, due to weather conditions, uncertain recording times over targets and other unforeseen events. We model this planning problem as the orienteering problem, which is a generalization of the traveling salesman problem. To cope with the environmental dynamics, we introduce the Two Stage Orienteering Problem (TSOP), which accounts for the effect of fuel uncertainty on the total objective value to be obtained during the UAV tour. To model and solve the TSOP we use techniques from stochastic programming. We will compare the TSOP approach to another UAV planning model based on robust optimization that was formulated in previous research. The results show that the TSOP model produces tours with a higher expected objective value than the tours resulting from the robust optimization method.
Maria Frolkova CWI M.Frolkova@cwi.nl Supervisor Abstract Bandwidth-sharing networks as considered by Massoulie & Roberts (1998,1999) are important flow level models of communication networks. We focus on the fact that it takes a significant number of users to saturate a link, necessitating the inclusion of individual rate constraints. In particular we extend work of Reed \& Zwart (2010) on fluid limits of bandwidth sharing with rate constraints under Markovian assumptions: we consider a bandwidth-sharing network with rate constraints where job sizes and patience times have a general distribution. We obtain a fluid limit in the general case. For monotone networks, we also establish interchange of limits, i.e. convergence of stationary distributions of the pre-limiting networks to the fixed point of the fluid limit. Kristiaan Glorie Erasmus University Rotterdam glorie@ese.eur.nl Supervisor Abstract Kidney exchanges have recently emerged as a way to alleviate the worldwide shortage of kidney donors. We study the centralized organization of kidney exchanges in a dynamic setting, where the timing of exchange is fixed but the arrival of patient-donor pairs is uncertain. Using robust optimization techniques, we derive optimal dynamic matching policies that are protected against this uncertainty. We make policy recommendations using simulations based on kidney exchange data from the Netherlands.
Derya Sever Eindhoven University of Technology D.Sever@tue.nl Supervisor Abstract Traffic network disruptions lead to significant increases in transportation costs. We consider a network in which a number of links are vulnerable, leading to a significantly higher travel time. For these vulnerable links, we consider known link disruption probabilities and knowledge on transition probabilities for recovering from or getting into a disruption. In this paper, we develop a framework based on dynamic programming in which we formulate and evaluate different policies as discussed in the literature. We also develop computation-time-efficient hybrid routing policies. In order to test the efficiency of these hybrid policies, we develop a test bed of networks with different characteristics and analyze the results of the policies. Our results show that an overwhelming part of the cost reduction is obtained by considering limited part of the network in detail. The performance of these hybrid policies only deteriorate slightly from the policies using more detailed information, e.g. only the time-dependent information, for the entire network.
Remy Spliet Erasmus University Rotterdam Spliet@ese.eur.nl Supervisor Abstract In our research we consider a vehicle routing problems in which time windows have to be assigned to each location before demand is known. Next, demand is revealed and a routing schedule has to be constructed, adhering to the time windows. This problem is encountered frequently in retail chains. The problem is solved to optimality using a branch-and-price algorithm. Lower bounds are obtained by solving the LP relaxation using a column generation algorithm.
Evelien van der Hurk Erasmus University Rotterdam EHurk@rsm.nl Supervisor Abstract Recently, data on individual passenger travel behavior has become abundantly available thanks to the current introduction of smart cards in many cities and countries around the world. Thanks to the wide adoption of smart cards for ticketing in public transport, data on individual passenger level has become available, providing information per person per journey, instead of aggregated information like vehicle loading. This research studies the possibilities this detailed smart card data provides for analyzing passenger flows and passenger behaviour. It focuses on combing the micro level of information of individual passengers with the macro level of aggregated passenger flows to obtain new knowledge and insight into passenger travel behavior, specifically focused on prediction of Origin Destination flows. The central research question is: Are patterns in travel behavior best extracted and explained by aggregated macro data on the train and OD-flow level, or by micro data on the journey and passenger level?} Our focus is on comparison and combination of micro and macro models for predicting passenger behavior,; and how a combination of micro and macro perspectives can lead to new insights in passenger behaviour in public transport. The analysis is based on smart card data from Netherlands Railways (NS), the largest passenger railway operator in the Netherlands.
Suzanne van der Ster Vrije Universiteit suzanne.vander.ster@vu.nl Supervisor Abstract We consider scheduling an implicit-deadline task system on a single machine in a mixed-criticality setting. Each task of such a system generates a (possibly infinite) string of jobs, released one by one, with an interarrival time bounded from below by a certain task-dependent period. Each job has a deadline equal to the length of that period. In a mixed-criticality setting, each task has multiple levels of worst-case execution time estimates and each task has its own criticality level j. By executing the tasks, we learn what level the system is in (which may change over time). When the system is in level k, all jobs of tasks of level larger or equal to k should be scheduled for their level-k execution requirement, to meet their deadline. Mixed-criticality systems arise when multiple functionalities are scheduled upon a single shared computing platform. This can force tasks of different importance (i.e. criticality) to share a processor. We give a scheduling algorithm for scheduling a mixed-criticality task system, called EDF-VD (Earliest Deadline First - with Virtual Deadlines), and analyze its effectiveness using the processor speedup metric. We show that if a 2-level task system is schedulable on a unit-speed processor, then it is correctly scheduled by EDF-VD on a processor of speed 4/3. We also give sufficient conditions to check feasibility efficiently. Finally, our results are extended to higher-level systems.
Antonios Varvitsiotis CWI A.Varvitsiotis@cwi.nl Supervisor Abstract The Gram dimension $\gd(G)$ of a graph is the smallest integer $k \ge 1$ such that, for every assignment of unit vectors to the nodes of the graph, there exists another assignment of unit vectors lying in $\oR^k$, having the same inner products on the edges of the graph. The class of graphs satisfying $\gd(G) \le k$ is minor closed for fixed $k$, so it can characterized by a finite list of forbidden minors. For $k\le 3$, the only forbidden minor is $K_{k+1}$. We show that a graph has Gram dimension at most 4 if and only if it does not have $K_5$ and $K_{2,2,2}$ as minors. We also show some close connections to the notion of $d$-realizability of graphs. In particular, our result implies the characterization of 3-realizable graphs of Belk and Connelly.
Eleni Vatamidou Eindhoven University of Technology e.vatamidou@tue.nl Supervisor Abstract Great attention is given in evaluating numerically the waiting time distribution of an M/G/1 or a G/G/1 queue. An important method is by approximating the service times with a phase-type distribution. What is usually not speci ed though is the number of phases needed in order to achieve a specified accuracy in the approximation of the waiting time distribution. In this presentation, we give the connection between the required number of phases and the speci ed accuracy we want to achieve for the waiting time distribution. Furthermore, we present an algorithm to approximate the waiting time distribution of an M/G/1 by approximating a completely monotone residual service time distribution with a hyperexponential one. For this approximation, we also provide error bounds. Finally, we compare our approximation with the heavy traffic and heavy tail approximations in the cases where service times follow a Pareto or a Weibull distribution.
Warren Volk-Makarewicz Vrije Universiteit Amsterdam wmakarewicz@feweb.vu.nl Supervisor Abstract The quantile function $q_\alpha$ yields for $\alpha \in (0,1)$ the value such that the probability of the event that a particular stochastic phenomenon, say X, is smaller than $q_\alpha$ is $\alpha$, i.e., $P(X \leq q_\alpha)=\alpha$. The quantile function is a well known performance measure for evaluating stochastic models. For instance, in asset management $q_\alpha$ is the amount under which the value of an assets within an investment fund will go with probability $\alpha$ (i.e., taking $\alpha=0.05, q_\alpha$ is an upper bound for the 5% smallest values of the asset), in manufacturing, the quantile function is applied for determining the quality margins for the six-\sigma quality control approach principle. In this talk we assume that the stochastic model under consideration can be influenced by some parameter $\theta$. For instance $\theta$ may be the correlation between pairs of stocks within the fund in an asset management model, or $\theta$ may be the breakdown rate of a machine in a manufacturing model. We will perform a sensitivity analysis of the quantile function with respect to $\theta$. Sensitivity analysis plays an essential role in the robustness analysis of stochastic models as it provides the means to analyze the influence of $\theta$ on the outcome of the model (if the model is too sensitive with respect to $\theta$, then the reliability of the model becomes questionable, if on the other hand the sensitivity is low, the model can probably by simplified). For our approach we determine a Monte Carlo estimator for the sensitivity of quantile function w.r.t $\theta$, at a given level $\alpha$, via Measure Valued Differentiation. We provide theory for (locally, at the quantile) continuous random variables, though it can be applied to results to discrete models. We also provide numerical examples and compare our estimator to other estimation techniques, particularly to perturbation analysis. Our estimator is of the single run type and does not require the otherwise typical res-simulation required by MVD.
Frederik von Heymann Delft University of Technology f.j.vonheymann@tudelft.nl Supervisor Abstract Integer linear problems are most commonly solved by first solving the linear relaxation and then applying certain strategies to obtain integer solutions from this. Among these strategies, cutting planes are very popular and successful for a large class of ILPs. We want to investigate under which circumstances these methods are slower than the size of the problem seems to indicate. One observation is that the presence of equalities can have unwanted effects, as here the feasible region of the problem (and its relaxation) lies in an affine subspace, while the cutting planes also take integer points outside this subspace into account. It therefore seems advisable to explore reformulations of the problem in the subspace. As the lattice restricted to this subspace is not the standard integer lattice, it becomes important to find a good basis for it, which ideally captures the shape of the feasible region, relative to the lattice. We will discuss different strategies to make use of this information.
Ihsan Yanikoglu Tilburg University I.Yanikoglu@uvt.nl Supervisor
Abstract This paper proposes a new way to construct uncertainty sets for robust optimization. Our approach uses the available historical data for the uncertain parameters and is based on goodness-of-fit statistics. It guarantees that the probability that the uncertain constraint holds is at least the prescribed value. Compared to existing safe approximation methods for chance constraints, our approach directly uses the historical-data information and leads to tighter uncertainty sets and therefore to better objective values. This improvement is significant especially when the number of uncertain parameters is low. Other advantages of our approach are that it can handle joint chance constraints easily, it can deal with uncertain parameters that are dependent, and it can be extended to nonlinear inequalities. Several numerical examples illustrate the validity of our approach.
Birol Yuceoglu Maastricht University b.yuceoglu@maastrichtuniversity.nl Supervisor Abstract The minimum triangulation problem is an NP-hard combinatorial optimization problem that has applications in Gaussian elimination of sparse matrices and vertex elimination in graphs. For a graph G=(V,E), finding a triangulation corresponds to obtaining a supergraph H=(V,E\cup F) where the addition of fill-in edges in F results in a chordal graph. The minimum triangulation problem corresponds to finding a triangulation H with the minimum number of fill-in edges and can be modeled as a perfect elimination ordering problem. In this study we analyze the facet structure of the perfect elimination ordering polytope and present a branch-and-cut algorithm for the minimum fill-in problem.
|