Abstract: I am mostly interested in algorithms for difficult combinatorial and geometric problems: What is the fastest tour from A to B? How to optimally assign jobs to machines? How can a robot move from one location to another one? Algorithms solving such problems are complex and their implementation is error-prone.

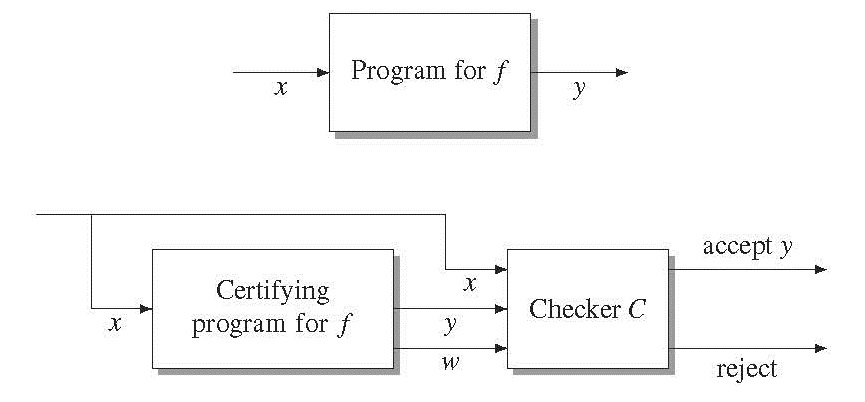
How can we make sure that our implementations of such algorithms are reliable? Certifying algorithms are a viable approach towards the goal. The top part of the figure above illustrates the I/O behavior of a conventional program for computing a function f . The user feeds an input x to the program and the program returns an output y. Why should the user believe that y is equal to f (x)?

A certifying algorithm for f computes y and a witness (proof) w; w proves that the algorithm has not erred for this particular input. The certifying algorithms is accompanied by a checker program C. It accepts the triple (x;y;w) if and only if w is a valid witness for the equality y=f (x). Certifying algorithms are the design principle for LEDA, the library of efficient data types and algorithms ([MN99]).

In the first part of the talk, we introduce the concept of certifying algorithms and discuss its significance.. In the second part of the talk, we survey certifying algorithms ([MMNS11]). In the third part of the talk, we discuss the formal verification of certifying computations ([ABMR14, NRM14]).

[ABMR14] E. Alkassar, S. B&\ouml;hme, K. Mehlhorn, and Ch. Rizkallah. A Framework for the Verification of Certifying Computations. Journal of Automated Reasoning (JAR), 52(3):241-273, 2014. A preliminary version appeared under the title "Verification of Certifying Computations" in CAV 2011, LCNS Vol 6806, pages 67-82.
[MMNS11] R.M. McConnell, K. Mehlhorn, S. Näher, and P. Schweitzer. Certifying algorithms. Computer Science Review, 5(2):119-161, 2011.
[MN99] K. Mehlhorn and S. Näher. The LEDA Platform for Combinatorial and Geometric Computing. Cambridge University Press, 1999.
[NRM14] Lars Noschinski, Christine Rizkallah, and Kurt Mehlhorn. Verification of certifying computations through AutoCorres and Simpl. In NASA Formal Methods Symposium, 2014.